Levenshtein distance: the similarity of two strings

2025-09-07 — 8 min read

Overview

The Levenshtein distance, one of several variations of “edit distance”, is a metric for measuring the similarity between two sequences or strings, defined by Soviet mathematician Vladimir Levenshtein in 1965.

Given two strings, e.g. “hello” and “world”, calculating the Levenshtein distance tells us the minimum number of single-character edits required to convert one string into the other. Three types of operation are permitted:

Deletion of a character,
Insertion of a new character,
Substitution of one character for another.

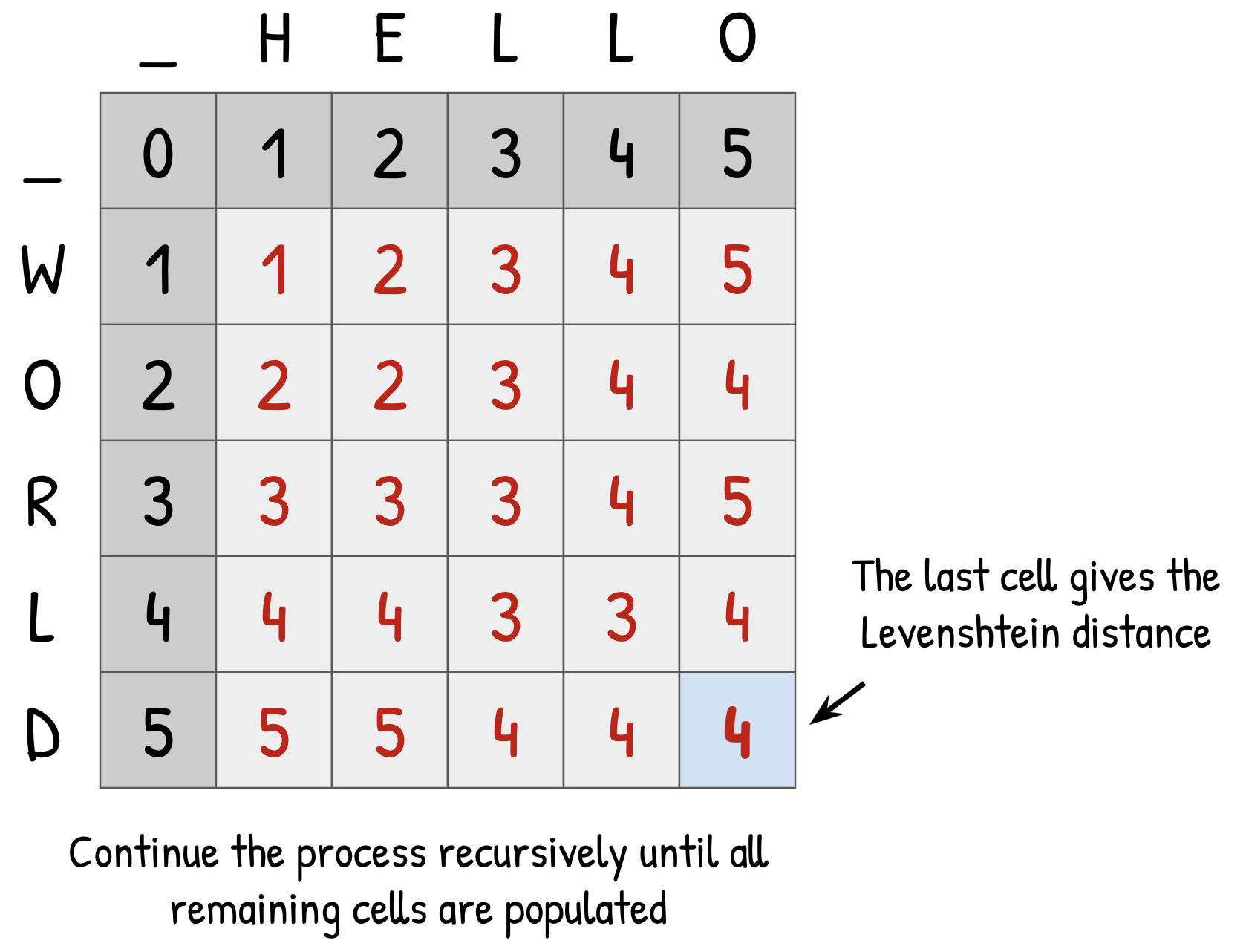
In the “hello/world” example we can see that both strings are five characters long, and there is one common character, the “l” at position four. The Levenstein distance between these two words is therefore four, since we need to swap the remaining letters.

Levenshtein distance is commutative (it does not matter in what order the strings are specified), and has clear upper and lower limits. If the strings are different lengths, then we will always need to either add or remove some characters, so this defines the minimum distance. If there are no common characters between the two strings, then all will need to be changed — the maximum distance is therefore the length of the longer string.

$$ |\text{len}(\text{A}) - \text{len}(\text{A})| \leq \text{Levenshtein distance} \leq \text{max}(\text{len}(\text{A}),\text{len}(\text{B})) $$

This distance measure has many applications from computer science to biology. For example, it finds use in automatic spell-checking when Microsoft Word suggests corrections; approximate string matching can be used in finding and ranking similar results to user input to a search engine; and it appears in computational biology in the comparison of DNA sequences.

Algorithm and example

A simple implementation to calculate the Levenshtein distance using dynamic programming techniques is the Wagner-Fischer algorithm. This uses a matrix to hold the cumulative distance as we traverse the two strings character by character.

Consider again the example “hello/world”. The algorithm is as follows:

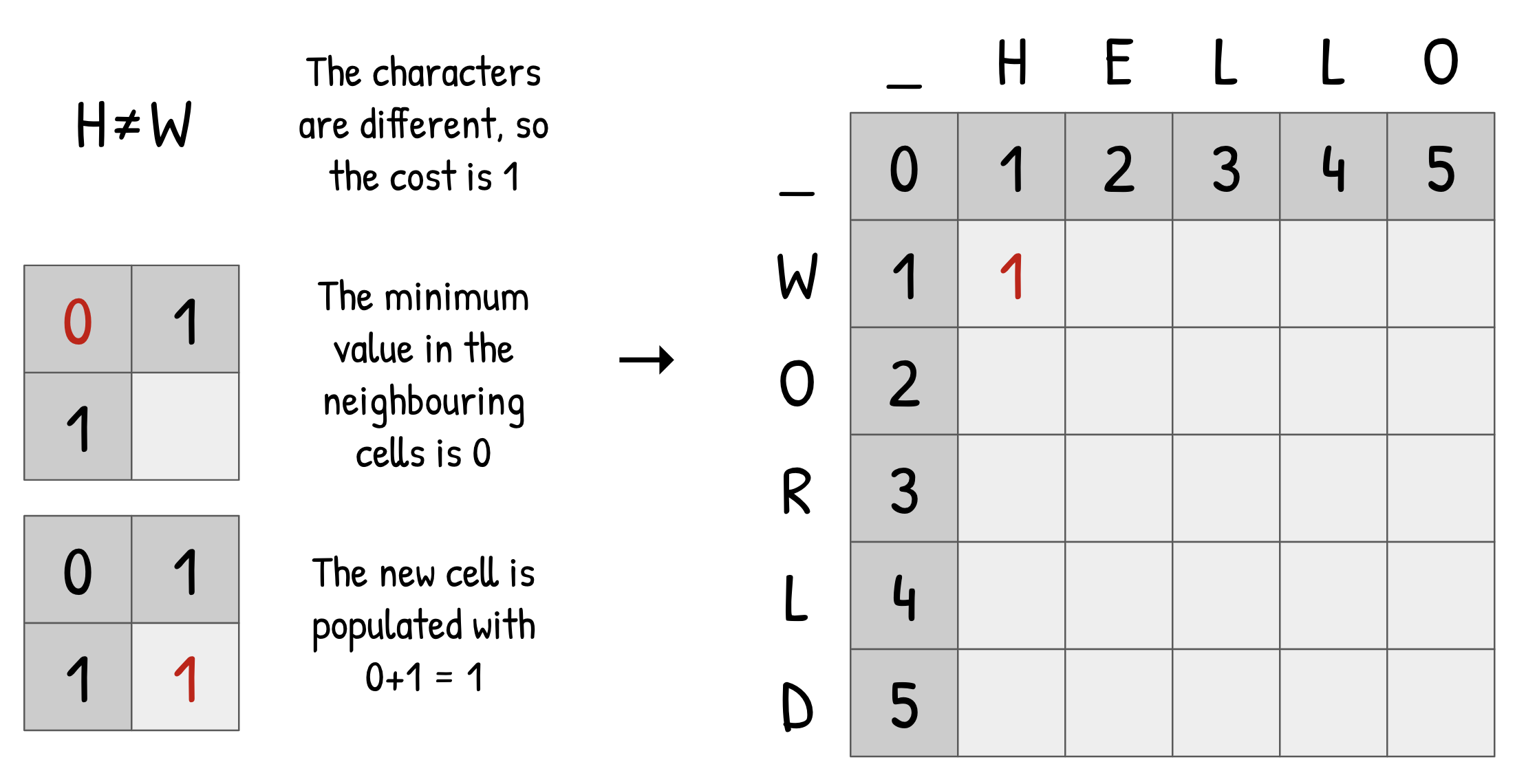
Begin by initialising a matrix with n+1 rows and m+1 columns, where n is the length of string A and m is the length of string 2. Here, each string has 5 characters and we have added an extra “empty string” character (shown above and to the left for clarity; he order of the words does not matter as the result will be the same).

Fill the first row and first column of the matrix with numbers 0-5. This represents how many characters must be inserted into the empty string in order to produce the substring at that point (“”=0, “h”=1, “he”=2, “hel”=3 and so on, and similar for “world”).

Beginning from the first empty cell on the top left, proceed from left to right and top to bottom.
1. For each cell, compare the character for this row and column. If the characters are the same, record a cost of 0. If they are different, record a cost of 1.
2. Record the minimum value out of the three cells immediately left, above, and above left of the current cell.
3. Fill in the current cell with this minimum value plus the cost (0 or 1), and proceed to the next cell.

Once all cells in the matrix have been filled in, the bottom right cell corresponds to the Levenshtein distance between the two strings.

Python script

The following python code is an implementation of the Wagner-Fischer algorithm, and will return the Levenshtein distance between two input strings.


  import numpy as np

  def levenshtein(string1, string2):
    rows = len(string1)+1
    cols = len(string2)+1
    matrix = np.zeros((rows, cols))
    matrix[...,0] = np.arange(rows)
    matrix[0,...] = np.arange(cols)
    for i in range(1,rows):
      for j in range(1,cols):
        if string1[i-1] == string2[j-1]:
          cost = 0
        else:
          cost = 1
        min_dist = min(matrix[i-1,j-1], matrix[i-1,j], matrix[i,j-1])
        matrix[i,j] = min_dist+cost
    return matrix[-1,-1].astype(int)

  print(levenshtein("hello", "world"))
  >> 4

Levenshtein distance: the similarity of two strings

Overview

Algorithm and example

Python script

Further reading